首先下文将会有这样的表述：红石激活与未激活(激活时会变成什么样子我不用解释了吧)分别记为“1”与“0”，或者“高电平”与“低电平”，或者“真”与“假”，在英文里就是“True”与“False”。这种二进制“非真即假”的表达就是“布尔逻辑代数”。

可能大家经常听到什么什么电器是“模拟”的，什么是“数字”的。这里的“数字的(Digital)”就是逻辑代数表达，因为只有两种状态，易于区分，抗干扰。比如我要通过信号传输告诉别人一个数字，比如说“50”，我用模拟信号的话，我规定50伏特的电压代表50——但传输到接受者那里，可能由于噪声干扰，50V就变成了49V，这样接收者就认为我发送的是49而不是50。所以模拟信号会受很大干扰。但是如果是数字信号，我用二进制的110010代表50，并规定大于40V就算逻辑“1”，小于10V就算逻辑“0”，然后发送出去——虽然可能消耗的时间是前面的6倍，但显而易见数字信号更抗干扰。所以其成为现代信息学的基石。下文中“取反”表示把0变成1，或把1变成0。“反相”也是类似的意思。

进入正题。逻辑门可以看作一个整体，只有输入端和输出端露在外面，而且你知道从输入到输出有什么样的关系，这就是逻辑门希望实现的。大规模的逻辑门组合可以实现复杂的运算。

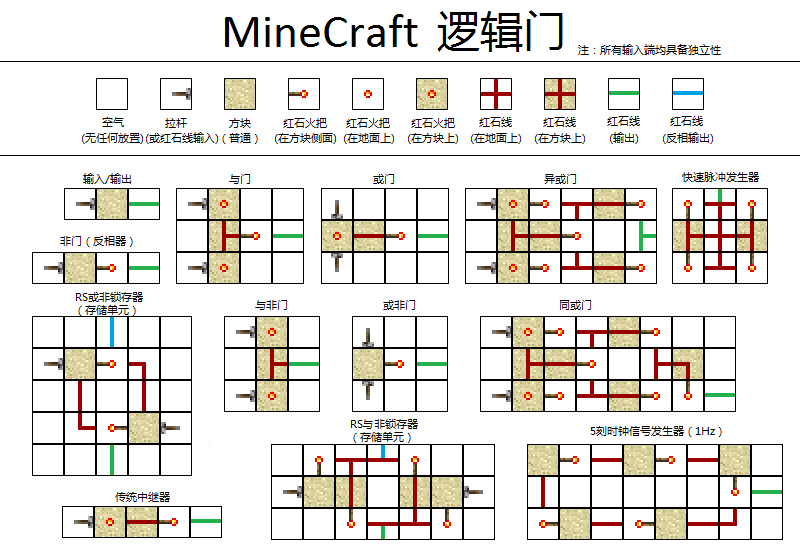
1、非门(NOT Gate)

非门有一个输入端，一个输出端。其作用是输出=反相输入。也就是输入0，输出1;输入1，输出0。一般当你财力窘迫到无力合成红石中继器时你也可以用首尾相接的两个非门达到延长传输距离的作用，须知“负负得正”嘛

2、与门(AND Gate)

与门有两个输入，一个输出。这样的话不同的输入有四种组合：00,01,10,11。但只有同时输入1的时候输出才是1，否则输出为0。这种特性可以有如此应用：一个输入端接拉杆，一个接按钮，与门输出端接你家大铁门——拉杆放在你身边，按钮放在门外。这样只有当你身边的拉杆输出为1时，按钮按下时门才会打开。拉杆就相当于一个“门锁”了。

3、或门(NOR Gate)

或门有两个输入，一个输出。只要任意一个输入为1，输出就是1。或门的结构甚是简单：

4、与非门(NAND Gate)

顾名思义，与非门就是与门的输出取反，效果与与门相反。只有两个输入全是1，输出才是0。WIKI图中的与非门设计实际上是把与门设计最右端的那个起到“非门”作用的红石火把移除的结果。输出端移除非门和加上非门的效果(除了延迟时间不同)是一样的!

5、或非门(NOR Gate)

同样顾名思义，或非门就是或门输出取反，效果与或门相反。只要任意一个输入为1，输出就是0。

6、异或门(XOR Gate)

这是个神奇的门：只有当两个输入不同，输出才是1。所以异或门有一个性质，就是你改变任意输入，输出都会改变。这可以应用在同时控制一扇门的两个开关上。任意时刻你切换任意开关，门都会作出反应。

7、同或门(XNOR Gate)

就是异或门输出取反得到。表现为两个输入相同，输出才是1。同样可以应用到双开关控制的一扇门的电路中。

下图第一行从左到右：与门，或门，非门。注意与门和或门的区别。

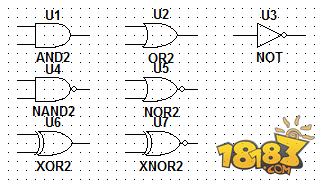
第二行：与非门，或非门。这行不用刻意去记忆——可以看到那一个小圆型代表的就是“取反”，就是主电路符号加上一个非门的简写——也正是因为这样，非门符号反而不多见。小圆型可以依附于任何大电路符号的输入端或者输出端，这时你就要注意信号的取反变化了。

第三行：异或门，同或门。注意写法。

图中所有门符号左端是输入端，右端是输出端。实际电路图中你要看门符号的朝向来判断哪些是输入端那些是输出端。尖端必然是输出端，单个逻辑门的输出端都只有一个。